Electricity is generated by a wide range of technologies. To compare their relative performance, the pros and cons of each are translated into a single economic variable: the generation cost per megawatt hour. As with any average, this cost hides considerable disparities and leads to political decisions based on poor economics.
The banishing of fossil fuels
If electricity consumers look at the changes in the cost of generating a MWh over the past decade (the attached graph gives an idea for the USA[1]), they will struggle to understand why wind and solar power have not yet pushed fossil fuels out of the electricity generation mix. These figures would suggest that doing so would help to reduce one’s energy bills. As for the politicians, they see the cost figures as a confirmation that green policies are the right way to go and declare that fossil fuels are on their way out.
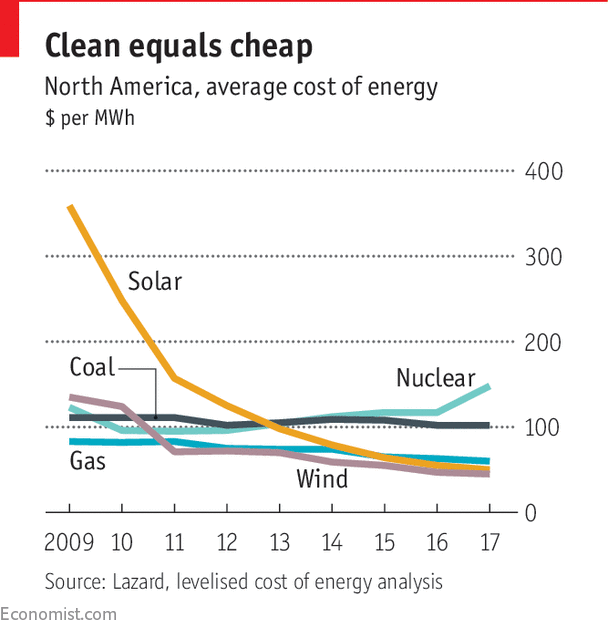
However, on a planetary scale, the dominant electricity generation technologies use coal (39%) and natural gas (23%), well ahead of hydro (16%), nuclear (10%) and renewable energies (7%).[2]
Leveling the costs
How can one hence explain why electricity suppliers have not adopted wind and solar generation whole-heartedly, if they are now far less expensive than fossil fuels? And why is it necessary to continue to subsidize green energies? The answer to these two questions lies in the highly misleading concept of cost, as used in the graph, known as "levelized cost of energy", or LCOE. With this estimate obtained by "smoothing" or "leveling", the cost is calculated as a ratio. The numerator is the present value of an investment and all the expenses entailed up to decommissioning (fuel, emissions quotas, maintenance, repairs, waste treatment, dismantling, etc.). [3] The denominator is the discounted quantity produced over the life of the facility.
This method of measuring the MWh cost should not be used for energies whose generation cannot be controlled, such as wind and solar, as it does not make sufficient allowance for generation timetables. In the calculation, time is taken into account only for the discounting of the flows, meaning the age of the operation. For example, with an annual discount rate of 5%, the monetary and physical flows expected in 10 years' time only account at present for half of their future value.[4] On the other hand, the exact date upon which each of the flows is documented is not taken into account. Therefore, for solar photovoltaics, the fact that the megawatt hours generated are all grouped together in the middle of the day has no influence on their cost. For any given facility located in any given place, if the megawatt hours were evenly spread throughout the day instead of being concentrated around the solar noon, their LCOE would have exactly the same value.
Smoothing by storage
The date energy is supplied on is an essential input for the calculation of its cost. The conditions of the generation (and therefore the cost) of a MWh in a coal-fired power station are almost the same at midday or at midnight, in August or in December, providing that the operator has sufficient stocks of coal. This is not true of solar photovoltaic or wind megawatt hours as the primary energy flows are not controlled by the operator. So, the variable production cost of the renewable MWh is zero (but for an unpredictable volume) when the sun shines and the wind blows, but it is infinite at night and at times of dead calm.
There are a number of ways of resolving this shortage of renewable energies on certain dates: adapting consumption to natural cycles (especially through pricing), importing energy from regions or countries where production conditions remain favorable when ours are not (they have a negative correlation), and resorting to fossil fuel power plants whose production can be stopped and started . However, as manufacturers, shopkeepers and households on their weekly food shop know too well, there is another technical solution for intermittent supply: storage.
It is of course not yet possible to store electricity directly. But the industry is developing other, indirect, storage methods, including gravitational (STEP), chemical (batteries), kinetic (flywheels), gaseous (hydrogen, synthetic methane) and heat (solar facilities, hot water boilers) sources.
All solutions to resolve intermittent supply come at a cost that is not included in the LCOE calculation. For example, on a photovoltaic micro-grid, the generation cost of a solar kWh deliverable at midnight is the cost of the panel that produces in the middle of the day added to the cost of the battery installed to transport that kWh from midday to midnight.[5]
On a national or continental grid, energy that is imported or generated in 'dispatchable' plants is more likely to be used to replace renewable sources when they are not available. This back-up combination of power stations and the grid therefore serves to guarantee supplies and its cost should be reflected in the total cost of renewable energies.
Profitability of intermittent energies
If the LCOE reflected the real costs of intermittent energies, it would no longer be necessary to subsidize them. Thanks to their low cost, they would replace other sources of energy on wholesale markets and supply contracts, and would make a profit. And yet, in 2018, the Contribution to the Public Electricity Service paid by the French consumer (€22.5 / MWh) will finance subsidies to renewables, paying €2.9 billion to the producers of photovoltaic power and €1.5 billion to the owners of wind farms.[6] This is because for wind and solar there is no economic calculation that would allow the operators to pocket the high prices for energy at times of peak demand. Sometimes, however, their output falls at just the right time. This is the case in the southern states of the USA, where the demand for electricity is at a maximum in the summer months for air-conditioning when the sun produces the most, which generates good revenues for solar PV operators. But in the European Union peak demand for electricity is in the winter, when the sun sets. And PV panels generate the most in summer, whereas demand from holidaymakers is low. The poor timing for these sales does not generate enough revenue for renewable energies to be able to forego subsidies.[7]
***
The LCOE is a useful costing model for comparing technologies with identical time profiles, for example different types of photovoltaic panels. But the truly relevant unit when it comes to electricity is not the MWh generated, it is the MWh delivered to a given place at a given time. The credibility of the commitments made to achieving such deliveries is not a good fit with the intermittent nature of renewable energies taken in isolation. So, one must add to the LCOE the dynamic and stochastic elements drawn from the costs of the complementary technologies needed to guarantee electricity supplied by intermittent sources.
[1] The Economist, 17 March 2018. The graph in The Economist is taken from a study by Lazard "Levelized Cost of Energy 2017", https://www.lazard.com/perspective/levelized-cost-of-energy-2017/
[2] https://www.connaissancedesenergies.org/les-chiffres-cles-de-lenergie-dans-le-monde-170926
[3] Estimates vary considerably depending on whether or not the environmental and grid connections costs are included. For solar photovoltaic, see "A review of solar photovoltaic levelized cost of electricity" by K. Branker, M.J.M. Pathak and J.M. Pearce, Renewable and Sustainable Energy Reviews 15 (2011) 4470– 4482. Interested readers may wish to download a calculator such as the one proposed by the Danish Energy Agency: https://ens.dk/en/our-responsibilities/global-cooperation/levelized-cost-energy-calculator.
[4] With this same discount rate, the expenses undertaken in 50 years currently only count for 10% of their future value, which explains why the financial provisions for dismantling are considered insufficient by environmentalists for whom future generations should be treated in the same way as the current generation. For them, the discount rate should be very low, or even zero.
[5] For the leveling of storage costs, see https://www.lazard.com/perspective/levelized-cost-of-storage-2017/
[7] On this subject, see the examples given by Paul L. Joskow in "Comparing the costs of intermittent and dispatchable electricity generating technologies", The American Economic Review, Vol. 101, No. 3, May 2011, pp. 238-241. http://ceepr.mit.edu/files/papers/Reprint_231_WC.pdf





