Jean-Pierre Florens has spent most of his career at the Toulouse School of Economics (TSE). With numerous coauthors he has made influential contributions to a wide range of different topics in econometrics and statistics, including treatment effects, Bayesian inference, econometrics of stochastic processes, causality, frontier estimation, econometrics of game-theoretic models, the GMM with continuum of moment conditions, the first rigorous treatment of the nonparametric instrumental variables regression as an ill-posed inverse problem, and more generally contributed to the development of the theory ill-posed inverse models in econometrics. He has published several monographs, including a rigorous first-year econometrics textbook, and has advised more than 50 Ph.D. students.
He is a Research Faculty of the TSE and Professor Emeritus, University Toulouse 1 Capitole. In addition to his extensive research in econometric theory, he has collaborated on many applied empirical projects in industrial organization, labor economics, forecasting traffic flows and correcting biases in radar altimeter measurements.
On a pleasant evening in mid-September we met with Jean-Pierre in the Place du Capitole in Toulouse on a terrace for drinks and afterward went out for dinner in a typical brasserie. It appeared to us that French food was the perfect setting to talk with one of France’s most influential econometricians. Lots of old stories emerged, but we also had spent much of that day seriously talking about his long, distinguished career. A fascinating career in fact, profound in depth and broad in breadth. We are happy to highlight some of it in this interview. Bon Appétit!
You grew up in Marseille. Tell us a bit about those years. What interested you in your early education?
I was born in Marseille in 1947 and I followed the usual French high school curriculum. I received my baccaloréat in 1964. I was good in mathematics but I was more interested in history and philosophy (I got two baccaloréats, one in mathematics and one in philosophy). I was also quite interested in politics and my first choice at the university was “Sciences Politiques” (in Aix-en-Provence). I originally did mathematics more as a hobby.
Interesting. We noticed that you have a Diplôme de l'Institut d'Études Politiques and another Diplome d’Études Supérieures de Science Économiques from Aix-Marseille. So, you studied primarily economics at the university during your undergraduate years? Subsequently, you obtained a doctorate in mathematics from the Université de Rouen. How did you make the transition from economics to math?

Figure 1: Conference celebrating the 65th birthday of Jean-Pierre Florens, Toulouse, September 28-29, 2012. Front row: Catherine Cazals, Jean-Marie Dufour, Hervé Ossard, Xiaohong Chen, Jean-Pierre Florens, Marine Carrasco, Costas Meghir, Marie-Hélène Dufour, Nour Meddahi. Second row: Guillaume Simon, Patrick Fève, Joel Horowitz, Frédérique Fève, Anna Simoni, Ingrid Van Keilegom, Leopold Simar, Senay Sokullu, Yacine Ait-Sahalia, Christian Nguenang, Pierre Dubois. Third row: Hajer Sayeh, Sophie Thibaut, Andreea Enache, Anne Péguin-Feissolle, Christian Bontemps, Richard Blundell, Whitney Newey, Anna Houstecka, Shuo Li. Fourth row: Enno Mammen, Olivier Faugeras, Chunan Wang, Qizhou Xiong, Yuichi Kitamura, Eric Gautier, Christian Gouriéroux, Christoph Bontemps, Costin Protopopescu, Gábor Uhrin. Last row: Qizhou Xiong, Serge Darolles, Jan Johannes, Thierry Magnac, Eric Renault, Vêlayoudom Marimoutou, Sylvain Chabé-Ferret, Pascal Lavergne, Jean-Marc Robin, Igor Kheifets, Debopam Bhattacharya, Vitalijs Jascisens.
It was not really a transition because I simultaneously studied three fields: economics, political science, and mathematics. I graduated with undergraduate degrees in each and masters in economics (on Bayesian econometrics) and mathematics (on algebraic topology). As a result of the dual master degrees, I had the choice between two possible areas for doctoral studies. I decided to stay in economics and went to CORE in Belgium, to do research in mathematical economics, which at the time was highly technical. My initial project was to work on the characterization of the set of equilibria in the case of a continuum of goods and agents. But in the end, I went back to Bayesian econometrics and statistics, again with the mathematical foundation being my main interest. I defended my thesis in mathematics and subsequently taught math, statistics, and econometrics to students in economics departments.
Can you tell us more precisely what was the subject of your doctoral dissertation? Who was your advisor?
In the old French system, there were two levels of dissertations: the “Thèse de troisième cycle” and the “Doctorat d’État”. For the former, I wrote a collection of papers on mathematical foundations of Bayesian statistics (sufficiency, identification, invariance), supervised by Jacques Voranger (Professor of Econometrics). For the latter, I wrote, under the supervision of Jean-Pierre Raoult (Professor of Mathematics), again on mathematical foundations of Bayesian statistics as well as on the Bayesian analysis of errors-in-the-variables models and limited information analysis of simultaneous equations models.
What was your inspiration to write Bayesian econometrics papers in the early part of your career?
My interest in the Bayesian approach in statistics came from my courses in economics and decision science taught by Professor Voranger (using the book by Raiffa and Schlaefer) and Bayesian statistics (using Degroot’s book). I became a teaching assistant for these courses and this is how Voranger became my advisor for my master’s degree on Bayesian analysis in the errors-on-variables models.
Presumably, those were rather unusual textbooks at the time to be used in the French system?
Absolutely. In fact, I approached statistics via the Bayesian approach and only discovered MLE and OLS after being taught the subjects of posterior distributions, the natural conjugate or the posterior odds. As I was well trained in measure theory and probability it was easy for me to make a transition to the Bayesian approach.
Your first published paper, co-authored with Michel Mouchart and Jean-Francois Richard, was on the Bayesian analysis of errors-in-the variables models. How did this collaboration come about?
My collaboration with Michel Mouchart and Jean-François Richard started at CORE during the academic year 1971-1972. During my stay, a seminar speaker claimed that in Bayesian analysis there was no distinction between the usual linear model and the error-in-variables model under a non-informative prior. This somewhat surprising result generated discussions between Michel, Jean-François and me. This was the origin of our first paper. Afterward, we also expanded our research and looked at what we called “linear models”, i.e. a class of models mixing the limited information approach (analysis of a partially structural set of linear equations) and factor analysis. This model has fewer equations than variables and required a precise definition of exogeneity and endogeneity. The discussions with Michel and Jean-François regarding these concepts started in 1975. In particular, the idea of defining exogeneity using the concept of cut was suggested by Michel after a seminar by Ole Barndorff-Nielsen.
CORE in Belgium was at the time, among other things, a center of excellence in Bayesian econometrics. Do you still remember your first visit?
Yes, indeed. I arrived at CORE in September 1971 as a research assistant. As mentioned earlier, I initially started working on mathematical economics. This was the time of abstract studies on general equilibrium and during the academic year 1971-1972 there was a special research effort at CORE focused on general equilibrium, with a lot of important visitors in the field, such as Gérard Debreu and Werner Hildenbrand, among others. Economics seminars at that time were quite different: speakers had to be precise about the topology of the spaces of goods and agents, for example.
But you moved back to econometrics?
Yes, I taught econometrics while visiting CORE, and my best friends were econometricians. This explains why I got back to econometrics. I should also say that I was a bit discouraged by my lack of progress on my research in general equilibrium theory. CORE was also a very stimulating place for research in Bayesian analysis of linear simultaneous equations, under the influence of Jacques Drèze and Anton Barten. The general idea was to get a family of tractable posterior distributions, named the poly-t.
This was before Monte Carlo integration techniques were widely adopted for Bayesian analysis?
Indeed. The idea was to integrate analytically the largest possible number of parameters in order to reduce the numerical complexity.
But this was probably still challenging, given computer technology at the time?
Well, I can tell you that Jean-François had a program for a system of two equations which required a supermarket caddy to carry around the punch cards. This tells you something about computer technology at the time as well as computational complexity.
Some people claim that your book with Mouchart and Rolin is one of the deepest books ever written on Bayesian analysis. Do you think this is a fair statement?
I must reluctantly admit that this is probably a fair characterization. As I was working with Michel and Jean-Francois on exogeneity, I also started to work with Jean-Marie Rolin and Michel on developing theoretical foundations of Bayesian statistics. The final result was the book “Elements of Bayesian Statistics”. The main interest of the book was to develop the algebra of the set of sub  -fields of a probability space in connection with the decomposition into marginal and conditional distributions. We treated systematically numerous concepts like completeness, separability, and invariance.
-fields of a probability space in connection with the decomposition into marginal and conditional distributions. We treated systematically numerous concepts like completeness, separability, and invariance.
Could you imagine back then that completeness would turn out to be useful for nonparametric identification?
No, at the time of writing the book we could not have imagined all the applications of our theory to inverse problems and IV estimation. One of the challenges of the book is that it is almost impossible to read a chapter in isolation, which discouraged many of our readers.
You ceased to work on Bayesian problems. What prompted that change of research focus?
There was an interruption of my work on Bayesian statistics but I returned to it more recently, in particular with my former PhD student Anna Simoni. Moreover, I was also not interested in pursuing the changing focus of Bayesian statistics on numerical analysis. I returned to the Bayesian approach via my recent interest in inverse problems, identification and GMM. The main feature of my papers on this topic pertains to using nonparametric statistics with Gaussian priors instead of Dirichlet priors or some extensions of Dirichlet processes. Note that this is in contrast to my earlier work with Jean-Marie where we did a lot of work involving Dirichlet processes. We look at asymptotic theory in this line of research. In particular, we consider posterior mean or distributions as estimators and study frequentist asymptotic properties of these objects such as concentration properties, von Mises theorem, adaptation, etc. I should also note that my original Bayesian papers were difficult to publish and they were often rejected for purely philosophical reasons as they were not mainstream Bayesian.
Let’s talk about the different people who – during your career – had an impact on your research. French econometricians of your generation were heavily influenced by the writings of Edmond Malinvaud. Did you interact with him? Did his famous econometrics textbook have any impact on your own research?
I have been strongly influenced by Edmond Malinvaud mainly indirectly by his books in econometrics but also on microeconomics. However, I have never worked at INSEE, ENSAE or CREST. I was invited several times by Malinvaud to his seminar and he always gave insightful comments. He agreed to be President of the committee of my Doctorat d’Etat. But in fairness, I was influenced more directly by Jacques Drèze during visits at CORE.
Perhaps we can also talk about how you met Claude Dellacherie. What did you learn from him?
In the old system of Doctorat d’Etat it was required to present the main thesis but the candidate was also supposed to give a seminar on a totally different topic a few months prior to the defense. My supervisor, Jean-Pierre Raoult Raoult proposed to Claude Dellacherie to give me a subject for this seminar. The topic was a characterization for the cut of Borelian sets in R2. This is an old topic in set theory, which started because of a mistake of Emil Borel which was pointed out by Yuri Linnik and Andrei Souslin. The complete result was proven at the end of the seventies by Dellacherie and Alain Louveau and I had to explain this result based on advanced set theory. Then I met Dellacherie several times before my defense. For me, it was the opportunity to study the book of Dellacherie and Paul-André Meyer and to improve my knowledge in abstract probably theory. His work had a very strong influence on my research in Bayesian statistics as it appeared in the book with Michel and Jean-Marie.
Another interesting person with whom you crossed paths Is Persi Diaconis. Most people probably don’t know about him. Apparently, he left a great impression on you. Can you tell us why?
You are right. I met Persi Diaconis during my three-month visit at the statistics department at Stanford University in 1981. I followed his seminar on advanced Fourier theory and we had many discussions on Bayesian statistics. I was impressed by Persi and by his research on many topics in probability and statistics. I invited him recently to give a seminar in Toulouse. I think his research on the consistency of Bayesian posteriors and on exchangeability is essential for statisticians.
You worked on so many different topics, causality, treatment effects, frontier estimation, ill-posed inverse problems, to name just a few. Do you mind if we talk about that?
Sure, go ahead.
The notion of causality in time series was a prominent research topic in the 70s and 80s with the influential work of Clive Granger, Chris Sims, and others. You published two Econometrica papers with Michel Mouchart on the topic which vastly expanded the notion of causality. Tell us about the origins of this research.
Well, my work on non-causality has two origins. As I said, we spent time working on exogeneity in the mid-70’s with Michel and Jean-François and we worked in particular on the extension of the concept of cut to dynamic models. The relationship between the different concepts of exogeneity in dynamic models required a notion of transitivity, which is, in fact, identical to Granger non-causality. Subsequently, I also worked on applications of this concept to macroeconomic models and we actually estimated the first VAR model for the French economy. This was not mainstream in France in the late 70’s as most researchers at the time worked with large simultaneous equation Keynesian models. Later on, joint with Denis Fougère, we realized that non-causality also has connections with martingale theory and therefore could be analyzed in continuous time. We always thought that the term “non-causality” is not adequate and we tried without success to use “transitivity” (which is also not very satisfactory) or “self-predictability”.
You also have a widely cited set of papers on nonparametric frontier estimation.
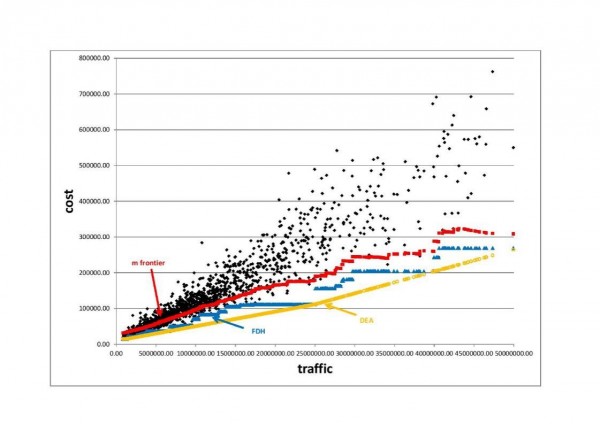
My interest in frontier estimation came from applications in the economics of the postal sector. More particularly we had access to a large data set on the cost of delivery offices and it was natural to estimate efficiency scores. We were faced with the usual problem of outliers and I had the idea of a concept of robust frontier (m-frontier) [1], where the estimation of an extreme is replaced by the estimation of an integral which simplifies the analysis of the statistical properties. Our contributions (with Leopold Simar and several co-authors) were essentially to combine the theory of frontiers and the statistical theory of extremes. I have always tried to treat econometric questions not in isolation, but to consider their mathematical or statistical foundations and to search for the most suitable tools (such as endogeneity and inverse problems or non-causality and decomposition of semi-martingales).
Treatment effects is a huge topic in the econometrics literature. You co-authored an Econometrica paper with Heckman, Meghir and Vytlacil. What led you to do research in this area?
I am glad you asked me this question. I am thinking about structural econometrics in the following sense: I assume that there exists a data generating process and that the difference between structural and reduced form approaches can be viewed as (functional) parameters we want to estimate or to test. In statistics (or in reduced form approaches) the parameters are “canonically” related to the DGP (distribution function, density, regression) but in the structural approach the definition of parameters comes from the economic model and such parameters are only implicitly related to DGP. This may, in fact, be the source of all identification problems. I think that econometricians (in particular micro econometricians) are not sufficiently focused on the reduced form parameters and I am not sure that, for example, the introduction of unobservable heterogeneity is always necessary. So, in the context of structural modelling, it is quite natural to look at treatment effect models. Moreover, it is not always easy to explain the endogeneity question to non-econometricians. The treatment effect model with continuous treatment is an excellent example to understand the issue of endogeneity.
For more than a decade you wrote extensively on ill-posed inverse problems in econometrics. This is still ongoing research. Can you tell us a bit about what fascinates you to work on this topic?
Well, I started to work on inverse problems at the end of the 90’s and presented the framework and its applications to instrumental variable estimation at the 2000 World Congress of the Econometric Society invited lecture in Seattle. The topic of non-parametric models with endogenous variables was on my mind at the beginning of the 80’s. At around the same time, non-parametric methods were introduced in econometrics, notably by Herman Bierens. During that time, I also proposed the topic to one of my PhD students, but unfortunately, we were not able to give a good answer to this question.
How did you come back to this topic?
After a while, I really started to look at inverse problems for three reasons. First, when I worked with Marine Carrasco on GMM with an infinite number of moment conditions we were faced with the inversion of the variance operator in order to define the optimal GMM. This was the first time we became familiar with Tikhonov regularization. A second motivation was a question coming from Philippe Gaspar working at the French spatial agency (CNES) on the analysis of satellite-based radar altimeter TOPEX-POSEIDON measurements of ocean levels. This analysis was essentially an estimation problem which required, in a non-parametric framework, solving a type II Fredholm equation. The third and final reason was my work with Eric Renault, Christian Gourieroux, Nizar Touzi, and Serges Darolles on the spectral analysis of diffusions. This research prompted me to get more acquainted with functional analysis. Instrumental variable problems
|
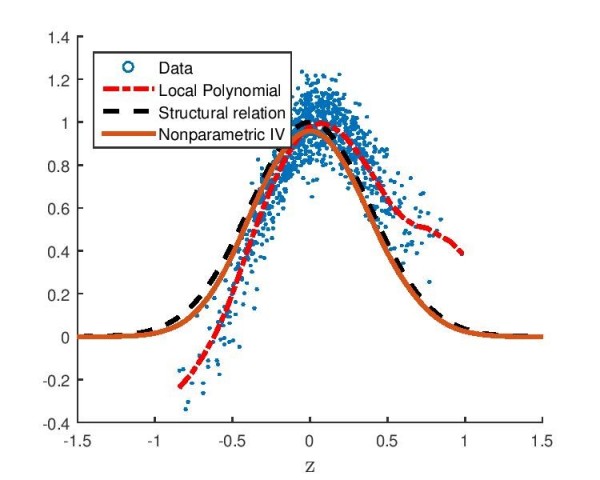
Figure 3: Endogeneity in the nonparametric regression and nonparametric IV. |
were a natural application. As I said before, my view of structural econometrics is to relate implicitly the objects of interest and the DGP. We are then naturally in a context of inverse problems and the GMM approach is a parametric application. This has the advantage of separating structural modelling (the construction of the implicit relation), the statistical part (the estimation of the DGP) and the “econometric” part, i.e. the resolution of the equation[2].
Note that this framework also applies to game theory settings where both ill- and well-posed problems may emerge. In fact, when it is well-posed the inversion may improve the statistical properties of the estimation of the DGP. Non-identified inverse problems also provide an alternative way to think about non-identification, where the identified sets are linear manifolds and with non-standard asymptotics.
For someone who has done so much research on non-parametric methods, what are your thoughts on the current literature using machine learning techniques?
I think that machine learning people have made extraordinary progress on algorithms and fast computational methods but with a rather naïve view of statistics and of econometrics. Machine learning seems to sometimes tackle intractable problems and give the appearance of providing reasonable solutions without a theoretical justification. Nevertheless, I admit that some topics in machine learning are interesting and useful for statisticians. For example, the use of Gaussian processes, the analysis of functional data or the interactions between geometry and statistics (estimation of the Laplacian for instance) should be carefully looked at by econometricians.
You supervised an amazing number of students throughout your career. More than 50, in fact, including many influential scholars. Tell us about your role as a mentor. What do you tell your students about doing research?

|
Figure 4: Recent Advances in Econometrics Conference, Toulouse 28-29 June, 2016. Front row: Pascal Lavergne, Tong Li, Koen Jochmans, Vitalijs Jascisens, Christian Bontemps, Sílvia Gonçalves, Andreea Enache, Christian Nguenang, Eric Gautier, David Pacini, Jean-Marie Dufour. Back row: Serge Nyawa, Robert Lieli, Christiern Rose, Philipp Ketz, Rohit Kumar, Andrii Babii, Nour Meddahi, Jules Tinang, Hiroaki Kaido, Christophe Gaillac, Patrik Guggenberger, Zhentong Lu, Brendan Kline, Federico Bugni. |
Indeed, I have supervised more than 50 PhD students and most of them have become academic researchers in many countries, including the USA, UK, Canada, New Zealand, Africa, and EU countries. The topics cover many fields of econometrics and many of my PhD students wrote dissertations motivated by applied econometric applications.
It is difficult to say if I am very directive. You should ask my former students. I typically spend a long time with my PhD students and I used to say that the supervision of advanced students was my main activity. I continue to work with many of them and a significant number of my papers are jointly written with PhD students or former students. I used to say to my students that research should be a regular activity: be in your office every day of the week, take breaks during the weekend and vacations and go regularly to seminars and conferences. I also suggest to teach (but not too much) and to work on several topics at once, and make sure that some are more easy in the sense that you know that you can find solutions in order not to be depressed by working only on very difficult topics. I am extremely happy to have created a group of former students all around the world and this has contributed strongly to the development of a Toulouse school of thought in econometrics.
Today the Toulouse School of Economics is an outstanding internationally renowned research center in economics. You were part of its creation. Can you tell us about the early days?

|
Figure 5: One of the first meeting in IO at Institut d'Économie Industrielle (IDEI), Toulouse, beginning of 90s. List of participants: Yacine Aït-Sahalia, Steven Berry, Alain Bousquet, Timothy Breshahan, Claude Crampes, Jacques Cremer, Glenn Ellison, David Encaoua, Jean-Pierre Florens, Denis Fougere, Jean Fraysse, Jose Garcia, Farid Gasmi, David Genesove, Christian Gollier, André Grimaud, Bronwyn Hall, Jerry Hausman, Ken Hendricks, Marc Ivaldi, Paul Joskow, Bruno Jullien, Fahad Khalil, Labonne, Jean-Jacques Laffont, Guy Laroque, James Levinsohn, Preston Mcafee, John McMillan, Thierry Magnac, David Martimort, Michel Moreaux, Steven Olley, Hervé Ossard, Harry Paarsch, Ariel Pakes, André de Palma, Robert Porter, Eric Renault, Patrick Rey, Jean-Charles Rochet, Diego Rodriguez, Nancy Rose, Bernard Salanie, Robin Sickles, Michel Simoni, Margaret Slade, Pablo Spiller, Jean Tirole, Daniel Vincent, Michael Vissier, Quang Vuong, Frank Wolak. |
I came to Toulouse in 1986 when Jean-Jacques Laffont suggested I apply for the position of professor of mathematics and statistics in Toulouse. This position was created in the Economics Department to support the newly created program “Magistère d’économiste statisticien”.
Jean-Jacques Laffont was himself also interested in econometrics.

|
Figure 6: Thèse d’état defense of Eric Renault in Toulouse at the end of 80’s. Jury: Jean-Charles Rochet, Jacques Lesourne, Jean-Jacques Laffont, Pierre-Marie Larnac, and Jean-Pierre Florens. |
Yes, Jean-Jacques was always interested in econometrics and he made several important contributions to econometrics. He believed that econometrics is a very important part of the economics department. Before I joined the department, Toulouse already had some tradition in econometrics (for example Quang Vuong spent some time in Toulouse working in particular with Jean-Jacques). We did not have senior scholars, but the group of young assistant professors in econometrics was very good. The development of this group took off in several directions. First, we recruited new people, like for example Eric Renault, or Thierry Magnac later. We supervised many PhD students in theoretical and applied econometrics. We obtained public research contracts (in particular on topics pertaining to labor markets) to finance the group and at the beginning of the 90’s Jean-Jacques created the Institut D’Economie Industrielle in order to develop partnerships with important companies. I worked with different firms and supervised a group of economists and econometricians working on the economics of the postal sector. The final step was the creation of the Toulouse School of Economics which increased our international visibility.
I am now emeritus. I don’t teach anymore and I am not allowed to supervise PhD students. I also stopped my consulting work with non-academic partners. My current research is focused on inverse problems, extreme values, and the relation between topological structures and statistics.
We thank you very much for sharing many of your insights and thoughts with us.
Selected publications
BOOKS
- Florens, J.P., Mouchart M. & J.-M. Rolin, “Elements of Bayesian Statistics”, M. Dekker, New York, 1990.
- Florens, J.P., Marimoutou, V., & Peguin, A., “Econometric Modelling and Inference”, Cambridge University Press, New York, 2007.
ARTICLES
Bayesian econometrics
- Florens, J.P., Mouchart, M., & Richard, J.-F., Bayesian Inference in Errors on Variable Models, Journal of Multivariate Analysis, 1974, 4, 419-452.
- Florens, J.P., “Expériences Bayésiennes Invariantes”, Annales de l’Institut Henri Poincaré, 1982, XVIII (4), 305-317.
- Florens, J.P. & Mouchart M., “Bayesian Specification Tests”, in Contributions to Operations Research and Econometrics the XXth Anniversary of CORE, B. Cornet and H. Tulkens (eds.), MIT Press, 1989, 467-490.
- Florens, J.P., Mouchart, M., & Rolin, J.-M., “Bayesian Analysis of Mixture : Some Results on Exact Estimability and Identification” in Bayesian Statistics IV, J. Bernardo, J. Burger, D. Lindley and A. Smith (eds.), North Holland, 1992, 127-145.
- Florens, J.P. & Mouchart M., “Bayesian Testing and Testing Bayesian”, in Handbook of Statistics, 10, G.S. Maddala (eds.), North Holland, 1992, 303-334.
- Florens, J.P., Larribeau, S., & Mouchart, M. “Bayesian Encompassing Test of a Unit Root Hypothesis”, Econometric Theory, 10(3-4), 1994, 747-763.
- Florens, J.P., Richard J.-F., & D. Hendry, “Encompassing and Specificity”, Econometric Theory, 1996, 12, 620-656.
- Florens, J.P. & Simoni A., “Nonparametric Estimation of an Instrumental Regression: a Quasi-Bayesian Approach Based on Regularized Posterior”, Journal of Econometrics, 2012, 170, 458-475.
- Florens, J.P. & Simoni A. “Regularized Posterior in Ill-posed Inverse Problems”, Scandinavian Journal of Statistics, 2012, 39, 214-235.
- Florens, J.P. & Simoni A. “Regularizing Priors for Linear Inverse Problems”. Econometric Theory, 2016, 31 (1), 71-121.
Dynamic models and stochastic processes
- Florens, J.P. & Mouchart, M., “A Note on Noncausality”, Econometrica, 1982, 50 (3), 583-591.
- Florens, J.P. & Mouchart, M., “A Linear Theory for Noncausality”, Econometrica, 1985, 53(1), 583-591.
- Florens, J.P. & Mouchart, M., “Conditioning in Dynamic Models”, Journal of Time Series, 1985, 6(1), 15-35.
- Florens, J.P., Mouhart M., & Rolin, J.-M., “Noncausality and Marginalization of Markov Processes”, Econometric Theory, 1993, 9, 239-260.
- Florens, J.P. & Fougère D., “Noncausality in Continuous Time”, Econometrica, 1996, 64(5), 1195-1212.
- Florens, J.P., Renault, E., & Touzi, N., “Testing for Embeddability by Stationary Scalar Diffusions”, Econometric Theory, 1998, 14, 744-769.
- Darolles, S., Florens, J.P., & Gouriéroux, C., “Kernel-Based Nonlinear Canonical Analysis and Time Reversibility”, Journal of Econometrics, 2004, 119(2), 323-354.
- Carrasco, M., Chernov, M., Florens, J.P., & Ghysels, E., “Efficient Estimation of General Dynamic Models with a Continuum of Moment Conditions”, Journal of Econometrics, 2007, 140, 529-573.
- Florens, J.P., Fougère, D., & Mouchart M. “Duration Models and Point Processes”, in The Econometrics of Panel Data L. Matyas et P. Sevestre (eds.) (3me édition), Springer, 2008, 547-601.
Frontier estimation
- Cazals, C., Florens, J.P., & Simar, L, “Nonparametric Frontier Estimation: A Robust Approach”, Journal of Econometrics, 2002, 106(1), 1-25.
- Florens, J.P., Simar, L., “Parametric Approximations of Nonparametric Frontiers”, Journal of Econometrics, 2005, 124(1), 91-116.
- Cazals, C., Fève, F., Florens, J.P., & Simar, L., “Nonparametric Instrumental Variables Estimation for Efficiency Frontier”, Journal of Econometrics, 2015.
- Florens, J.P., Daouia, A., & Simar, L., “Functional Convergence of Quantile-Type Frontiers with Applications to Parametric Approximations”, Journal of Statistical Planning and Inference, 2008, 138(3), 708-725.
- Carrasco, M., Florens, J.P., & Renault E., “Linear Inverse Problems in Structural Econometrics. Estimation based on Spectral Decomposition and Regularization”, Handbook of Econometrics, J. Heckman and E. Leamer, 6B, chapter 77, 2007, 5633-5751.
- Florens, J.P., Daouia, A., & Simar, L., “Frontier Estimation and Extreme Values Theory”, Bernouilli, 2010, 16 (4), 1039-1063.
- Florens, J.P., Daouia, A., & Simar, L., “Regularization of Non Parametric Frontiers”, Journal of Econometrics, 2012, 168, 285-299.
- Florens, J.P., Van Keilegom, I., & Simar, L., “Frontier Estimation in Nonparametric Location-Scale Models”, Journal of Econometrics, 2014, 178, 456-470.
Ill-posed inverse problems
- Carrasco, M. & Florens, J.P., “Generalisation of the GMM to Continuous Time Models”, Econometric Theory, 2000, 16(6), 797-834.
- Florens, J.P., “Inverse Problems and Structural Econometrics: The Example of Instrumental Variables”, in Advances Economics and Econometrics, Theory and Applications, Eighth World Congress of Econometric Society, Seatle, 2000, Volume 2, M. Dewatripont, L. P. Hansen and S. Turnosky (eds.), Cambridge University Press, Cambridge, UK, 2003, 284-311.
- Carrasco, M., Florens, J.P., & Renault, E., “Asymptotic Normal Inference in Linear Inverse Problems”, in Handbook of Non Parametric Statistics, J. Racine, L. Su and A. Ullah (eds.), Oxford, 2014, 65-96.
- Florens, J.P., Johannes, J., & Van Bellegem, S., “Identification and Estimation by Penalization in Nonparametric Instrumental Regression”, Econometric Theory, 2011, 27(3), 472-496.
- Carrasco, M. & Florens, J.P., “Spectral Method for Deconvolving a Density”, Econometric Theory, 2011, 27(3), 546-581.
- Darolles, S., Fan, F., Florens, J.P., & Renault, E., “Non Parametric Instrumental Regression”, Econometrica, 2011, 79(5), 1541-1565.
- Florens, J.P. & Sokullu, S., «Non Parametric Estimation of Semi Parametric Transformation Models”, Econometric Theory, 2017, 33, 839-873.
- Benatia, D., Carrasco, M., & Florens, J.P., “Functional Linear Regression with Functional Response”, Journal of Econometrics, 2017, 201 (2), 269-291.
Econometrics of game theoretic models
- Florens, J.P., Hugo, M.A., & Richard, J.-F., “Game Theory Econometric Models: Application to Procurements in the Space Industry”, European Economic Review, 1997, 41(3-5), 951-960.
- Armantier O., Florens, J.P., & Richard, J.-F., “Approximation of Bayesian Nash Equilibrium”, Journal of Applied Econometrics, 2008, 23(7), 965-981.
- Florens, J.P. & Sbaï, E., “Local Identification in Empirical Games of Incomplete Information”, Econometric Theory, 2010, 26(06), 1638-1682.
- Dunker, F., Florens, J.P., Hohage, T., Johannes, J., & Mammen, E., “Iterative Estimation of Solutions to Noisy Nonlinear Operator Equations in Nonparametric Instrumental Regression”, Journal of Econometrics, 2014, 178, 444-455.
- Fève, F. & Florens, J.P., “Nonparametric Analysis of Panel Data Models with Endogenous Variables”, Journal of Econometrics, 2014, 181(2), 151-164.
- Carrasco, M. & Florens, J.P., “On the Asymptotic Efficiency of GMM”, Econometric Theory, 2014, 30(2), 372-406.
- Florens, J.P. & Bellegem, S., “Regularized Estimation of Linear Functional Models”,. Journal of Econometrics, 2015, 186 (2), 465-476.
- Florens, J.P. & Enache, A., “Nonparametric Estimation for Regulation Models”, Annals for Economics and Statistics, 2017.
- Florens, J.P. & Enache, A., “Identification and Estimation in a Third-Price Auctions Model” conditionally accepted for Econometric Theory.
Others
- Florens, J.P., Ivaldi, M., & Larribeau, S., “Sobolev Estimation of Approximate Regressions”, Econometric Theory, 1996, 12, 753-772.
- Florens, J.P. & Gaspar, P., “Estimation of the Sea State Bias in Radar Altimeter Measurements of Sea Level: Results from a Non-Parametric Method”, Journal of Geophysical Research, 1998, 103, 15, 803-814.
- Florens, J.P., Foucher, C., “Pollution Monitoring: Optimal Design of Inspection. An Economic Analysis of the Use of Satellite Information to Deter Oil Pollution”, Journal of Environmental Economics and Management, 1999, 38, 81-96.
- Florens, J.P., Fève, F., Cambon-Thomsen, A., Eliaou, J.F., Gouraud, P.A., & Raffoux, C., “Evaluation Economique de l’Organisation d’un Registre de Donneurs de Cellules Souches Hématopoïétiques”, Revue d’Epidémiologie et de Santé Publique, N° 55, 2007, 275-284.
- Florens, J.P., Heckman, J., Meghir, C., & Vytlacil, E., “Identification of Treatment Effects Using Control Functions in Model with Continuous Endogenous Treatment and Heterogenous Effects”, Econometrica, 2008, 76(5), 1191-1206.
[1] The m-frontier is the expected value of the minimum of the costs of a random drawing of m units of productions producing more than a given level of outputs”. Resulting m-frontier estimator is robust to outliers unlike classical FDH/DEA estimators, see Figure 2.
[2] The nonparametric IV regression is defined by the conditional moment restriction and solves an ill-posed functional equation. It is a structural parameter with causal interpretation, unlike the conditional mean function. Resulting nonparametric IV estimator corrects for endogeneity, unlike the local polynomial estimator on Figure 3.



